- THERMO-IONIQUE (ÉMISSION)
- THERMO-IONIQUE (ÉMISSION)L’émission thermo-ionique telle qu’elle est comprise aujourd’hui est une branche de la physique qui traite des divers phénomènes liés à l’éjection d’électrons d’un corps solide chauffé à une température suffisamment élevée. On substitue maintenant souvent à ce terme traditionnel le terme plus correct d’émission thermoélectronique . Il y a plus de deux cents ans, on découvrit que l’air, au voisinage des corps chauds, pouvait conduire l’électricité. Puis, vers 1897, Joseph John Thomson montra que les particules chargées émises par du carbone chauffé à haute température dans le vide étaient des électrons. Les progrès réalisés ensuite par la technique du vide ont permis, d’une part, d’éliminer un certain nombre de phénomènes parasites tels que l’empoisonnement de l’émission par les gaz résiduels, les contaminations de surface et, d’autre part, d’utiliser de façon reproductible et fiable l’émission thermo-ionique, en particulier dans les tubes électroniques.Les fondements théoriques sont maintenant bien établis en ce qui concerne les métaux purs, et des progrès remarquables ont été effectués pour les alcalino-terreux, bien que de nombreuses inconnues subsistent encore.Émission des métaux pursÉquation fondamentale de l’émission d’électronsLe modèle physique décrivant l’émission d’électrons est dû à Arnold Sommerfeld. D’après ce modèle, un cristal d’un métal est assimilé à un puits de potentiel contenant un gaz dégénéré d’électrons qui occupent dans le puits de potentiel un certain nombre d’états énergétiques. On peut calculer le nombre d’états d N qui occupent une énergie comprise entre E et E + d E:
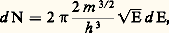Les électrons, qui se déplacent librement dans le métal et occupent différents niveaux d’énergie, ne peuvent s’échapper du métal, car ils sont retenus par des forces électriques à la surface de ce dernier. Le nombre d’électrons dn par unité de volume dans le métal et leur répartition énergétique sont donnés par le produit de la fonction de distribution de Fermi f par le nombre d’états possibles d N:
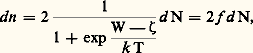où k est la constante de Boltzmann et T la température absolue.Le facteur 2 vient du fait que deux électrons peuvent occuper chaque niveau d’énergie avec leurs signes en opposition; W est l’énergie d’un niveau permis mesurée depuis le fond de la bande de conduction, 﨣 est le niveau d’énergie en dessous duquel tous les niveaux d’énergie sont occupés par des électrons à T = 0. Le nombre probable dn d’électrons ayant des vitesses comprises entre vx et vx + d vx , vy et vy + d vy , vz et vz + d vz est: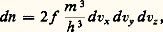
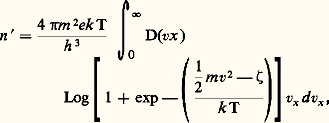où D(vx ) est la probabilité pour qu’un électron approchant la barrière de potentiel à la surface du métal avec une vitesse vx puisse passer dans le vide.En ce qui concerne D(vx ), il est nécessaire de connaître la forme de la barrière de potentiel à la surface. À cet effet, on peut écrire que l’énergie potentielle W(x ) d’un électron de charge e situé à une distance x de la surface en présence d’un champ électrique E est:
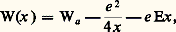où Wa désigne l’énergie au niveau de Fermi. À champ nul, on a la courbe (a) de la figure 1 et, lorsque le champ varie, on a les courbes (b).Soit 淋 = 連e E la variation du potentiel de sortie due à l’effet de champ. En première approximation, seuls les électrons ayant une énergie supérieure à Wa 漣 e 淋 franchiront la barrière de potentiel et les autres seront réfléchis:
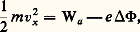ce qui donne respectivement:
si l’on a:
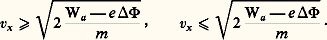Cependant, cette loi n’est pas parfaite, car un petit nombre d’électrons qui ont une énergie supérieure à Wa 漣 e 淋 sont aussi réfléchis. On tient compte de ces effets en écrivant:
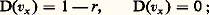le coefficient de réflexion r est choisi indépendant de vx . La densité de courant j en présence d’un champ électrique E pour une surface homogène s’écrit, 淋 étant le travail de sortie (cf. infra ),
et, à champ nul,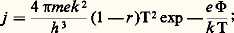
cette dernière équation est appelée l’équation fondamentale de Richardson-Dushman .Le coefficient A = 4 神mek 2/h 3 vaut théoriquement 120 A 練 cm-2 練 K-2, ce qui n’est pas vérifié expérimentalement, car la surface n’est jamais complètement uniforme et le travail de sortie dépend de la température selon la relation:
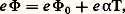ce qui donne A = A0 exp(face=F0019 漣 見e/k ).On constate que, sauf pour le césium, les valeurs de A données dans le tableau 1 sont égales environ à la moitié ou au quart de la valeur théorique. Les nombreuses recherches entreprises pour expliquer ces valeurs expérimentales n’ont pas encore abouti.Travail de sortieLe travail de sortie est celui qu’il faut fournir à l’électron pour lui permettre de vaincre la barrière de potentiel (cf. effet PHOTOÉLECTRIQUE). Le travail de sortie de la plupart des métaux est mesuré par émission thermo-ionique ou par effet photoélectrique. Les méthodes théoriques pour sa détermination ont, grâce à des chercheurs tels que E. P. Gyftopoulos, J. D. Levine, N. Razor, G. Hatsopoulos, fait des progrès sensibles. Les relations qu’ils ont établies servent à déterminer le travail de sortie dans le cas d’absorption de gaz ou de métaux sur d’autres métaux (tungstène, césium, par exemple). On utilise en général l’équation de Richardson-Dushman et la relation précédente qui donne 淋 en fonction de T en prenant 見 = 2 練 10-5 à 8,8 練 10-4 K-1, entre 600 et 1 000 K, et en tenant compte de l’orientation cristalline du métal (tabl. 2).Distribution des vitesses des électronsÀ l’intérieur du métal, le nombre d’électrons dn ayant une vitesse comprise entre vx et vx + d vx , etc. est donné par la loi de distribution de Fermi indiquée plus haut.Le nombre d’électrons émis qui auront une vitesse comprise entre v x et v x + d v x , etc. est:
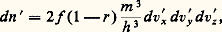ou encore, avec une très bonne approximation,
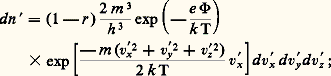cette distribution de vitesse est maxwellienne.La vitesse quadratique moyenne des électrons est donnée par (1/2)m v2 漣 k T, ce qui, dans le cas présent, donne:
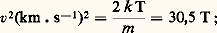la vitesse de l’électron est de 175 km 練 s-1 à 1 000 K.Effet de champChamp accélérateurIl existe toujours un champ électrique du fait de la différence de potentiel entre l’émetteur et l’électrode adjacente, et ce champ tend à accélérer les électrons émis. Cependant, une fraction d’entre eux, d’autant plus importante que la tension accélératrice est plus basse, est, par suite des effets de répulsion mutuelle des électrons, repoussée vers la cathode. Le courant augmente donc avec la tension appliquée à température constante, et jusqu’à la saturation. Si l’on continue d’augmenter le champ électrique, on observe d’abord une croissance assez lente du courant de saturation, puis, au-delà de valeurs de champs supérieures à 10-5 cm-1, la cathode devient le siège d’un autre type d’émission, l’émission de champ. Dans le premier cas, on a affaire à l’effet Schottky et, dans le second cas, à l’effet de champ ou effet Fowler-Nordheim .La limitation du courant émis par les effets de répulsion mutuelle des électrons (effets de charge d’espace) a été analysée par Child et Langmuir, qui ont montré qu’il apparaît devant la cathode un minimum de potentiel Vm situé à une distance Xm de la surface de la cathode.Child et Langmuir ont établi une équation pour le courant à charge d’espace j c en tenant compte de la relation:
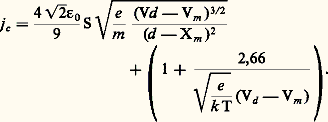On utilise plus simplement dans la pratique l’équation suivante:
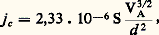où S est la surface de la cathode et VA le potentiel appliqué.La grandeur j c VA size=1漣3/2, qui ne dépend que de la forme de la diode et qui s’appelle la pervéance , vaut, dans une diode plane, 2,33 練 10-6 (S/d 2).Champ retardateurSupposons maintenant que le champ soit retardateur. Seuls les électrons ayant une vitesse suffisante pour vaincre ce champ pourront atteindre l’électrode adjacente. Le courant en champ retardateur émis j r est:
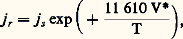où j s est le courant de saturation. D’autre part, V, potentiel effectif, est:
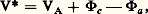où VA, 淋c et 淋a désignent respectivement le potentiel appliqué, le potentiel de sortie de la cathode et le potentiel de sortie de l’anode.La figure 2a montre des courbes représentant les différents cas et la figure 2b les diagrammes d’énergie relatifs aux trois cas.Émission des corps polycristallinsDans la pratique, on a rarement affaire à des monocristaux, les métaux étant toujours polycristallins, et, comme on l’a vu, la densité de courant dépend du travail de sortie, donc de l’orientation; le courant émis sera donc la somme de tous les courants émis par les différents cristaux. Le travail de sortie sera un travail de sortie moyen e 淋 漣, égal à la moyenne de tous les travaux de sortie des différents cristaux présents sur la surface. La figure 3 montre un exemple d’une surface polycristalline de molybdène.Émission de métaux avec couche adsorbéeDepuis les expériences de Langmuir sur l’adsorption du césium sur le tungstène, on a compris que des films adsorbés pouvaient avoir un effet très important sur l’émission d’électrons. Le mécanisme peut être décrit comme suit. Si le potentiel d’ionisation de la couche adsorbée est de l’ordre du potentiel de sortie du métal de base, ou supérieur à lui, la couche adsorbée diminue le potentiel de sortie de ce dernier. On peut aussi avoir l’effet inverse, des atomes qui ont une affinité électronique suffisante pouvant par exemple accroître le potentiel de sortie (cas de l’oxygène sur le tungstène). La loi générale est:
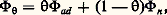où 淋n est le potentiel du métal nu, 淋 size=1 celui du métal avec un taux de recouvrement et 淋ad le potentiel du métal avec une monocouche complète.Aspect pratiquePour son emploi dans les tubes électroniques, un émetteur thermoélectronique doit posséder de nombreuses qualités, à savoir:– pouvoir émissif élevé (quelques micro-ampères à plusieurs dizaines d’ampères par centimètre carré en impulsion),– durée de vie suffisante (plusieurs dizaines de milliers d’heures),– bon rendement,– bonne résistance mécanique,– faible tension de vapeur,– résistance suffisante au bombardement ionique.Le problème est de trouver un matériau dont la vitesse d’évaporation reste admissible lorsqu’on le chauffe à haute température pour lui faire émettre des électrons. Le choix de l’émetteur est ainsi déterminé grâce à un compromis entre ces deux qualités.On classe les cathodes en deux grandes catégories: les cathodes à structure simple et les cathodes à structure complexe. Les cathodes à structure simple sont les cathodes en métal pur, les cathodes à couches minces adsorbées et les cathodes constituées d’un métal recouvert d’une couche épaisse homogène. Le tableau 3 donne un aperçu de leurs propriétés. Les cathodes à structure complexe se subdivisent en deux grandes catégories, l’une dérivant des perfectionnements des cathodes à oxydes, l’autre comprenant des cathodes dites à réservoir (tabl. 4).Toutes ces cathodes sont utilisées dans les tubes électroniques tels que diodes, triodes, penthodes, klystrons, carcinotrons, tubes à ondes progressives, lasers, thyratrons, etc., et tous ces tubes fonctionnent avec des champs accélérateurs.Il faut cependant signaler une utilisation particulière des cathodes à couches adsorbées, constituées par le convertisseur thermo-ionique. Ce tube fonctionne sans champ électrique appliqué. Le principe en est simple: on chauffe un émetteur d’électrons, de préférence en tungstène, face à une électrode. L’ensemble est placé sous vide dans une pression partielle de vapeur de césium. Les électrons qui ont une énergie thermique suffisante franchissent la barrière de potentiel et sont recueillis par le collecteur. Il apparaît alors aux bornes des deux électrodes une différence de potentiel qu’on appelle différence de potentiel de contact. On dispose ainsi d’un générateur à basse tension et à courant élevé (0,7 V et 7 A 練 cm-2). On sait réaliser à l’heure actuelle des diodes ayant des surfaces de 60 cm2. L’énergie nécessaire au chauffage peut être d’origine solaire (en plaçant l’émetteur au foyer d’un miroir concave), d’origine chimique (en plaçant l’émetteur dans une flamme d’essence) ou d’origine nucléaire (en plaçant le convertisseur dans le cœur d’un réacteur nucléaire). On peut, à l’aide de ce dernier moyen, construire des générateurs de plusieurs dizaines de kilowatts électriques sans pièce tournante.
Encyclopédie Universelle. 2012.
